viernes, 12 de julio de 2013
martes, 21 de mayo de 2013
PENSAMIENTO GEOMÉTRICO
La geometría estudia los cuerpos,
sus propiedades, las relaciones existentes entre ellos, las propiedades y las
características del espacio que permanecen invariantes a través de posibles
transformaciones de las figura; estudia también el espacio, los objetos que en
él se encuentran y sus movimientos.
El objetivo de la enseñanza de la geometría en la
escuela es ayudar al alumno a dominar sus relaciones con el espacio para que
pueda representar y describir en forma ordenada el mundo en que vivimos y
conocer los entes geométricos como modelizaciones de la realidad. El punto de
partida de ese conocimiento es el tratamiento intuitivo de las
nociones espaciales y geométricas. La construcción del significado de los
conceptos espaciales y geométricos se lograra a través de su utilidad para
resolver problemas.
FLORES DE PAPEL CON LA TÉCNICA DEL ORIGAMI
A ti que te encantan las flores y la técnica del origami entonces te encantará esta manualidad. Te mostraré cómo hacer flores con la técnica del origami: es muy sencillo, ¡solo presta atención!
Hoy haremos honor al arte oriental del origami con unas bellas flores de papel. Estas flores quedan muy bonitas para decorar cualquier rincón de tu hogar cuando acabas de hacerlas. Sigue leyendo y aprende cómo hacerlas ahora mismo.
Materiales:
·
Papel
o cartulina
·
Pistola
de silicona
·
Palito
de brochette
Paso a paso:
Para hacer flores
de papel en origami, lo primero que debes hacer es tomar un
trozo de cartulina cuadrado y doblarlo a la mitad por la línea diagonal,
formando un triángulo.
Ahora lleva las dos puntas de este triángulo
hacia arriba, de manera de formar nuevamente un cuadrado. Dobla ambas puntas
del triángulo.
Toma las puntas que acabas de doblar para
volver a formar un cuadrado y esta vez dóblalas verticalmente hacia afuera.
¿Ves? Es así como debe
quedarte cuando dobles las dos puntas hacia afuera del cuadrado. Esta es la
forma que buscamos.
Con tu dedo levanta las esquinas que doblaste en el paso anterior. Mete
el dedo dentro de la cartulina para levantar las esquinas.
Ahora aplasta estas
esquinas con tus manos.
Mete la punta de las esquinas dentro de la parte que acabas de aplastar,
así quedará más prolijo
Toma las dos partes de la cartulina con las que vienes trabajando y
dóblalas por lo largo.
Con la pistola de silicona pega una parte con la otra para formar una
especie de forma cónica
Así te quedará cuando
acabes de pegarla. Este será uno de los pétalos de la flor. Para completar la
flor, debes hacer aproximadamente cinco de estos pétalos. Luego pegalos todos
juntos lado a lado y une estos en el palito de brochette.
Flores
en origami paso a paso: ¡no te pierdas el vídeo!
En caso de que te hayan quedado dudas mira este vídeo instructivo para
ver el paso a paso en acción
Puedes hacer varias flores de papel con origami y atarlas todas juntas para formar un
hermoso ramo de flores de papel.
lunes, 20 de mayo de 2013
TABLERO MATEMÁTICO
HISTORIA DEL ORIGAMI.
Origami
significa "doblar papel". Y lo definimos diciendo que el origami es
el arte de hacer objetos mediante el uso de hojas de papel.
Su origen
proviene de China y las primeras figuras de origami se remontan al período
Heian (794-1185).El siglo VI traspasó las fronteras y llegó a Japón
En sus
inicios sólo estaba reservado a las clases altas ya que el papel era escaso.
Los
sintoístas, religión que rinde culto a las fuerzas de la naturaleza y a los
antepasados, usaban mariposas de papel en sus ritos matrimoniales, siendo el
símbolo de unión intima y amor constante
Las figuras
clásicas del origami vienen del Período Edo (1600-1898). Para ese entonces el
origami ya no tenía sentido religioso, sino de diversión.
En esta
época nacieron las grullas, libélulas, mariposas, ranas y monos.
En general,
la tradición del origami se transmitía de padres a hijos
La primera
recopilación fue hecha en 1845 y se llama "Kan no modo"
Pero
el origami no sólo atrapó a Japón, sino que también consiguió atrapar a
los musulmanes, quienes fueron impactados por todo lo que se podía llevar a
cabo con un simple trozo de papel.
Expulsados
los musulmanes de España el origami siguió quedándose en esas tierras para
luego extenderse a Sudamérica con las expediciones de Colón y finalmente a todo
el mundo.
Entre los
fanáticos del origami están
El poeta
británico Percy Shelley (1972-1822).
El autor de
"Alicia en el país de las maravillas", Lewis Carroll (Inglaterra,
1832-1898).
El pedagogo
alemán Frederich Fröbel (1782-1852), creador del kinder.
El filósofo
español Miguel de Unamuno (1864-1936)
José Ortega
y Gasset (1883- 1955).viernes, 22 de febrero de 2013
domingo, 17 de febrero de 2013
TALLER "DONALD EN EL PAÍS DE LAS MATEMÁTICAS"
VÍDEO: DONALD EN EL PAÍS DE
LAS MATEMÁTICAS
LUEGO DE LO OBSERVADO EN EL VÍDEO RESPONDE A LAS SIGUIENTES PREGUNTAS:
1. ¿Qué te pareció la película?
2. ¿Qué aspectos relacionados con las matemáticas has encontrado?
3. ¿Qué te ha llamado más la atención? ¿Agregarías algo? ¿Por qué?
4. En este fantástico viaje al país de
las matemáticas, a lo largo de la película se hacen referencia a distintas
personas, acontecimientos lugares reales; realiza un breve comentario de los
siguientes aspectos: Pitágoras, los pitagóricos y la música; El número de oro;
El rectángulo áureo en la naturaleza; las matemáticas en los juegos y el
significado del infinito.
.jpg)
.jpg)
.jpg)
viernes, 15 de febrero de 2013
INSTRUMENTOS DE AYUDA
http://recursostic.educacion.es/multidisciplinar/itfor/web/sites/default/files/recursos/poliedrosycuerposredondos/html/actividad_1_clasificacin_de_poliedros_y_cuerpos_redondos.html
lunes, 11 de febrero de 2013
DATOS CURIOSOS DE LOS NÚMEROS
1.1. Un gramo de veneno de una Cobra puede matar a 150 personas.
Una sola pila puede contaminar 175.000 litros de agua.
Una vuelta al mundo puede dar la unión de venas, arterias y vasos del cuerpo humano.
1:45 horas llevaba cocinar un pollo en las cocinas de carbón o leña en
el año 1860. Hoy, en un horno a microondas esto se redujo a 15 minutos.
3 bebés por segundo nacen aproximadamente en el mundo.
Cada 3 horas se abre un McDonald's en
algún lugar del mundo.
3,20 metros es la altura que puede saltar un canguro.
8 ojos tienen las arañas
8 a 9 mm. por año es la velocidad con la que la Torre de Pisa se está inclinando
9 días puede vivir una cucaracha sin su cabeza, hasta que muere... de
hambre.
Tomado de:
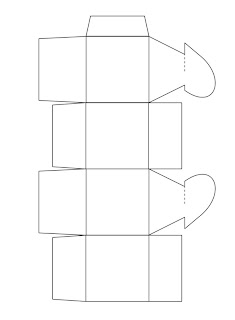
MANUALIDAD PARA ELABORAR
CAJA DE DULCES
¡Sorprende a tus amigos y familiares
con sus dulces favoritos dentro de esta
adorable caja! Es un trabajo realmente sencillo y económico: muy fáciles de
hacer, y que puedes obsequiar en cualquier ocasión.
Puedes decorarlas luego a tu gusto
con papeles, cintas, dibujos, un mensaje. Aquí como siempre te damos la idea,
luego tú la sigues a tu antojo. ¡Comencemos!
Materiales:
·
Cartulina
rosa para niñas o azul para niños el color lo escoges tú.
·
Lápiz
·
Regla
·
Tijera
·
Pegamento en
barra
Dulces
1. Copia el molde de la caja o su contorno en la
cartulina rosa o azul. Recórtalo delicadamente.
2. Con ayuda de la regla, comienza a marcar los dobleces según
indica el molde.
3. Coloca pegamento en los laterales correspondiente y luego
puedes ir armando la caja siguiendo los pliegues que habías marcado.
4. Antes de cerrar la cajita, guarda los bombones (o lo que
quieras) adentro.
¡Pronto! Ya tienes tu
caja en cartulina, un detalle de amor muy lindo. Repite el
procedimiento para hacer muchas más y seguir sorprendiendo. ¿No te parece súper
tierna?
tomado de: http://www.lasmanualidades.com/2007/08/21/cajas-romanticas-muy-faciles-de-hacer
TABLERO MATEMÁTICO
PENSAMIENTOS MATEMÁTICOS
PENSAMIENTO NUMÉRICO Y SISTEMAS NUMÉRICOS
Este estándar describe la comprensión profunda y fundamental del conteo, del concepto de número y de las relaciones aritméticas como también los sistemas numéricos y sus estructuras. Involucra los conceptos y algoritmos de la aritmética elemental así como las propiedades y características de las clases de números que son el comienzo de la teoría de números. También incluye la proporcionalidad y el concepto y uso de las fracciones. Lo central de este estándar es el desarrollo del sentido numérico, la habilidad de descomponer números de manera natural, el uso de las operaciones matemáticas para resolver problemas, la comprensión del sistema decimal, la estimación, el sentido numérico y el reconocimiento de las magnitudes relativas y absoluta de los números. En el desarrollo de este estándar se prepara a todos los estudiantes para: • Comprender los números, las formas de representarlos, las relaciones entre ellos y los sistemas numéricos. • Comprender el significada de las operaciones y como se relacionan unas con otras. • Hacer cómputos de manera fluida y estimaciones razonables.
Suscribirse a:
Entradas (Atom)